Problem

"You came across a custom server that Dr Xernon's company eleCTRic Ltd uses. It seems to be storing some encrypted files. Connect with nc 2018shell2.picoctf.com 15037. Can you get us the flag?" Source

Solution

The title makes a clear reference to AES-CTR. We can see that this mode of AES requires a unique nonce for each encrypted value to remain cryptographically secure. If we look at the problem's source code, we can see that the counter remains constant for all values. This breaks the encryption used and we are able to reveal the keystream and encrypt arbritary data.

class AESCipher(object):
    def __init__(self):
        self.bs = 32
        random = Random.new()
        self.key = random.read(AES.block_size)
        self.ctr = random.read(AES.block_size)

    def encrypt(self, raw):
        cipher = AES.new(self.key, AES.MODE_CTR, counter=lambda: self.ctr)
        return cipher.encrypt(raw).encode('base64').replace('\n', '')

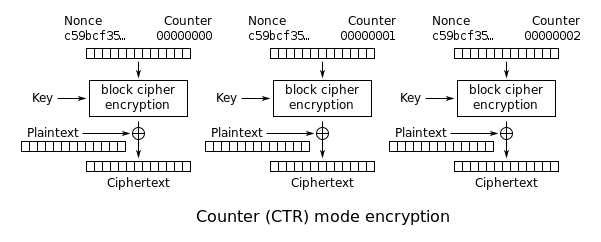
AES-CTR simply XORS the plaintext with the keystream (a value derived from the key and the counter).

To understand the exploit, it is important to know the following XOR rules (where ⊕ indicates XOR): $$ a \oplus a = 0 \ a \oplus b = b \oplus a \ (a \oplus b) \oplus c = (c \oplus b) \oplus a $$

AES-CTR can be understood as the following, where F is some deterministic function:

$$ C = P \oplus F(key, nonce) $$

Given the following: $$ P_1 = \text{plaintext 1} \ C_1 = \text{ciphertext 1} \ P_2 = \text{ciphertext 2} $$ It is possible to find $C_2$.

$$ C_1=P_1 \oplus F(key, nonce)\ $$ We can rearrange the equation to the following: $$ C_1 \oplus P_1 = F(key, nonce) $$ Then we can subsitute $C_1 \oplus P_1$ for $F(key, nonce)$ $$ C_2 = P_2 \oplus F(key,nonce)\ C_2 = P_2 \oplus C_1 \oplus P_1 $$

We are able to arbitrarily encrypt any data we want if we have two cipher texts with the same nonce.

Solve Script

from base64 import b64decode, b64encode

flag_file = "" # The value to encrypt
known_plaintext = "ABCDEFGHABCDEFGHABCDEFGHABCD" + ".txt"
known_cipher_b64 = "d8bImO+u0C2MOOfGkfdOoHfGyJjvrtAtjDjnxvrFcZw=" # The encrypted version of known_plaintext
known_cipher = b64decode(known_cipher_b64)

print("known_cipher length %d" % len(known_cipher))

#Encryption and decryption are symmetric operations; encrypting a ciphertext will reveal its value
def encrypt(key, plaintext):
    ret = bytearray()
    for i in range(0, len(plaintext)):
        ret.append(key[i%len(key)] ^ ord(plaintext[i]))
    return ret

#Calculate the key-stream from the known cipher and the known plaintext
key = bytearray()
for i in range(0, 32):
    key.append(known_cipher[i] ^ ord(known_plaintext[i]))


print("key %s" % key)
print("key length %d" % len(key))

#Verify the encryption remains the same for the known_plaintext
print(b64encode(encrypt(key, known_plaintext)))
#Print actual encrypted text
print(b64encode(encrypt(key, flag_file)))